Teil 2 - Standardnormalverteilt
Das zweite Tutorial zum Thema Zufallszahlen geht auf die standardnormalverteilten Zufallszahlen ein und baut auf den ersten Teil "Zufallszahlen erzeugen 1. Teil" auf.
Was heißt nun "Standardnormalverteilt"?
Normalverteilt heißt einfach ausgedrückt, daß sich die zu generierenden Zahlen ungefähr glockenförmig (siehe auch "Gaußsche Glockenkurve") verteilen. Also vom Ausgangspunkt (Erwartungswert) verteilen sich die Zahlen dichter und werden mit zunehmender Größe eher seltener vorkommen.
Dazu verwendet dieses Tutorial die Polar-Methode die vom Mathematiker George Marsaglia entwickelt wurde. Mit dieser Methode werden aus zwei gegebenen gleichverteilten Zufallszahlen y1 und y2 zwischen 0 und 1(!) zwei standardnormalverteilte unabhängige Zufallszahlen z1 und z2 erzeugt.
Die Formel:
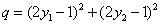
Ist q > 1, muss erneut ein q-Wert erzeugt werden und zwar solange bis q ≤ 1 ist. Dann berechnet man
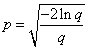
Zum Schluß ergeben sich die beiden standardnormalverteilten Zufallszahlen z1 und z2 so:
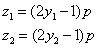
Für die Prüfung und Wiederholung bis q ≤ 1 ist wird ein rekursiver Ansatz verwendet.
1. Funktionsansatz... Entwurf
(defun :m-PolarMethod-TMP (/ p q y1 y2 z1 z2)
(setq y1 (car (:m-rand 1))
y2 (car (:m-rand 1))
)
(cond
((<= (setq q (+ (expt (- (* 2 y1) 1) 2) (expt (- (* 2 y2) 1) 2)))
1
)
(setq p (sqrt (/ (* -2 (log q)) q)))
(setq z1 (* (- (* 2 y1) 1) p)
z2 (* (- (* 2 y2) 1) p)
)
(list z1 z2)
)
('else (:m-PolarMethod-TMP))
)
)
Kürzen wir nun die Funktion und reduzieren die Variablen...
;Erzeugt aus zwei gleichverteilten Zufallszahlen
;zwei standardnormalverteilte Zufallszahlen
;sexy coded by Rolf Wischnewski
(defun :m-PolarMethod (/ yi q)
(setq yi (:m-rand 2))
(cond
((<= (setq q (apply '+ (mapcar '(lambda (n) (expt (- (* 2 n) 1) 2)) yi))) 1)
(mapcar '(lambda (i) (* (- (* 2 i) 1) (sqrt (/ (* -2 (log q)) q)))) yi)
)
('else (:m-PolarMethod)
)
)
)
Wie schon oben erwähnt benötigt dieser Algorithmus zwei gleichverteilte Zufallszahlen zwischen 0 und 1. Hierzu ruft diese Funktion die bereits im Zufallszahlen erzeugen 1. Teil gezeigte Funktion :m-rand auf, die wiederrum die Funktion :t-seed benötigt.
Zur Vervollständigung hier die beiden Funktionen nochmal gezeigt...
;Erzeugung eines Seed Wertes als initialen Wert x
;für die Generierung von Zufallszahlen
(defun :T-Seed ()
(cond (*seed*)
((setq *seed* (getvar "date")))
)
)
;Erzeugung einer Liste mit gleichverteilten Zufallszahlen zwischen 0 und 1
;Argumente:
;#len = Länge der zu generierenden Liste
(defun :m-rand (#len / retlst)
(repeat #len
(setq retlst
(cons
(/ (setq *seed* (rem (+ (* 25173 (:t-seed)) 13849) 65536))
65536.0
)
retlst
)
)
)
)
Aufruf der Funktion :m-PolarMethod ...
(:m-PolarMethod) => (0.0827171 0.288013)
(:m-PolarMethod) => (0.515879 -1.18094)
(:m-PolarMethod) => (1.26437 -0.620201)
(:m-PolarMethod) => (1.74086 1.45232)
(:m-PolarMethod) => (-1.48973 1.68383)
(:m-PolarMethod) => (-0.191413 -0.457987)
(:m-PolarMethod) => (-2.63655 0.719923)
Beispiel:
Um sich die Normalverteilung bildlich vorzustellen, werden wir zufällige Punkte um einen gewählten Punkt erzeugen. Wir setzen dabei die DrawPoints Funktion in leicht abgeänderter Version ein (alle nötigen Funktionen aus dem ersten Tutorial sind implementiert), die uns ein Bild von der Gleichverteilung zeigte.
;Argumente
;#PointSet = Punktmenge (Anzahl der zu zeichnenden Punkte)
;#Point = Punkt als Liste (getpoint)
;#Limit = Punktausbreitung
;sexy coded by Rolf Wischnewski
(defun DrawPoints (#PointSet #Point #Limit / :m-RndLimit
:m-RoundToEven
:M-3d2d
:PO-addPoint
)
;; local functions
(defun :m-RndLimit (#lrnd #LowerLimit #UpperLimit)
(mapcar '(lambda (rnd)
(+ (* (- #UpperLimit #LowerLimit) rnd) #LowerLimit)
)
#lrnd
)
)
(defun :m-Round (#real)
(cond ((= 'real (type #real))
(if (<= 0.5 (abs (rem #real 1)))
(if (> #real 0)
(1+ (fix #real))
(1- (fix #real))
)
(fix #real)
)
)
(#real)
)
)
(defun :m-RoundToEven (#numlst)
(mapcar '(lambda (n)
(if (/= (rem n 1) 0.5)
(:m-Round n)
(progn (if (> n 0)
(* 2 (:m-Round (/ n 2)))
(* 2 (:m-Round (/ n 2)) -1)
)
)
)
)
#numlst
)
)
(defun :M-3d2d (3dpt)
(list (float (car 3dpt)) (float (cadr 3dpt)))
)
(defun :PO-addPoint (#p #col)
(entmake (list (cons 0 "POINT") (cons 10 #p) (cons 62 #col)))
)
(defun PointList (#PointSet #Point #Limit / retval)
(repeat #PointSet
(setq retval (cons (mapcar '+
(:M-3d2d #point)
(:m-rndlimit
(:M-POLARMETHOD)
0
(fix #Limit)
)
)
retval
)
)
)
)
;;body
(:PO-addPoint #point 1)
(foreach p (PointList #PointSet #point #Limit)
(:PO-addPoint p 7)
)
(prin1)
)
Aufruf:
(DrawPoints
300
(setq *point* (getpoint " Bitte einen Punkt klicken"))
(getdist *point* " Ausbreitung festlegen")
)
Print-Ergebnis:
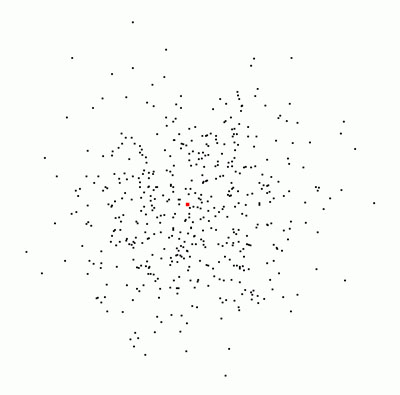
Wie auf dem Bild gut zu erkennen ist, werden die schwarzen Punkte um den roten Punkt herum dichter verteilt und je größer die Entfernung vom Zentrum ist, seltener erzeugt. Es ensteht eine Glockenkurve... (siehe Gaußsche Glockenkurve)
Mit Hilfe dieser Funktion könnte man eine Vegetation rund um einen See erzeugen (Büsche, Bäume ...etc.) oder auch einen künstlich angelegten Wald generieren. Mit einer Gleichverteilung würde das Ergebnis nicht so prickelnd aussehen.
Als Abschluß zum Thema "Rund um Zufallszahlen" hier noch ein Link mit einem anschaulichen Beispiel aus der Praxis, der die Normalverteilung von Zufallszahlen in Verbindung mit Varianzwerten aufzeigt => Statistik Normalverteilung: Gewicht Hühnereier
Mit freundlicher Genehmigung von Rolf Wischnewski. Originalbeitrag im Juli 2006, CADmaro.de
