Vor kurzem suchte ich nach einer einfachen Möglichkeit, um die Koordinaten des Mittelpunktes Schwerpunkt) eines Dreiecks zu bestimmen. Die Lösung ist denkbar einfach...
Mit linearer Algebra lässt sich sowohl der Satz als auch die nachfolgende Regel über die Koordinaten des Schwerpunktes recht einfach zeigen.
Die Koordinaten des Mittelpunktes (Schwerpunkt) sind das arithmetische Mittel der Koordinaten der Eckpunkte.
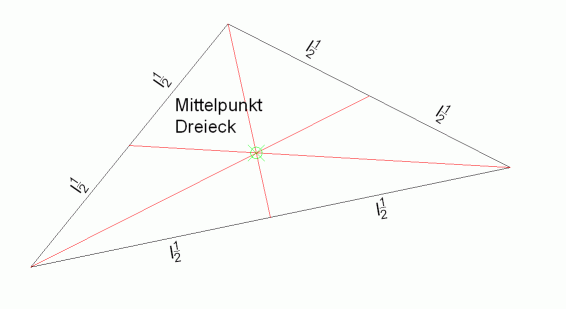
Das Dreieck ABC sei mit den Koordinaten seiner Eckpunkte gegeben.
A = (xA|yA)
B= (xB|yB)
C= (xC|yC)
Bilden wir jetzt die nötige Formel dazu
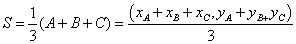
und nun bringen wir das ganze in eine Lisp Funktion. Erstmal als Grundgerüst, weiter unten optimieren wir den Code natürlich.
(defun dreieckmitte (#p1 #p2 #p3 / mitte xp xp1 xp2 xp3 yp yp1 yp2 yp3)
(setq xp1 (car #p1)
xp2 (car #p2)
xp3 (car #p3)
yp1 (cadr #p1)
yp2 (cadr #p2)
yp3 (cadr #p3)
)
(setq xp (/ (+ xp1 xp2 xp3) 3)
yp (/ (+ yp1 yp2 yp3) 3)
)
(setq mitte (list xp yp))
)
Wir addieren jeweils die x und y Werte und teilen das Ergebnis durch 3. Die Funktion gibt zum Schluss den Mittelpunkt als Koordinate zurück, indem wir die berechneten Werte (xp und yp) als Liste ausgeben.
Optimieren wir obenstehenden Code dahingehend, dass wir keine setq's mehr benötigen. Die Addition der Koordinaten erledigen wir mit einem mapcar. Als Ergebnis erhalten wir eine neue Liste und auf diese Liste führen wir wieder ein mapcar aus indem wir alle Werte dieser Liste durch 3 dividieren. Als Rückgabe erhalten wir nun den Mittelpunkt (x y z).
(defun TriangleCenter (#p1 #p2 #p3)
(mapcar
'(lambda (x) (/ x 3))
(mapcar '+ #p1 #p2 #p3))
)
Damit haben wir unsere Funktion zur Bestimmung des Mittelpunktes (Schwerpunkt) eines Dreiecks, doch halt...
wir können hier noch etwas feilen.
Sind A1, A2, ... An endlich viele Punkte (in der Ebene oder im Raum), so wird ihr Schwerpunkt als
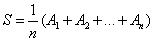
beschrieben.
Also, physikalisch entspricht S dem Massenmittelpunkt einer endlichen Menge von (gleich schweren) Massenpunkten. Verbinden wir diese Punkte miteinander so ergibt sich daraus ein regelmäßiges Vieleck.
Was sind regelmäßige Vielecke?
Ein regelmäßiges Vieleck hat n Ecken, n gleich lange Seiten und n gleich große Innenwinkel.
(Die Variable n steht für eine natürliche Zahl größer als 2.)
Deren Mittelpunkt ist gleichzeitig der Mittelpunkt eines Kreises in dem das Vieleck einbeschrieben ist.
Darstellung eines regelmäßigen Vielecks hier 7-Eck.
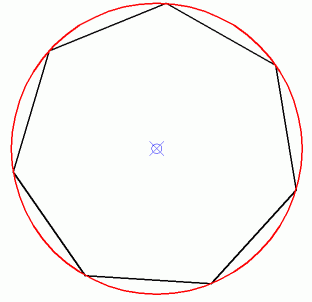
Auch hier gilt der gleiche Satz wie oben: Die Koordinaten des Mittelpunktes (Schwerpunkt) sind das arithmetische Mittel der Koordinaten der Eckpunkte.
Wir müssen also nur unsere Funktion auf die neue Situation anpassen. Dabei übergeben wir nun eine Liste mit Punkten.
(defun regularpolycenter (#LstOfPoints / tmp)
(setq tmp '(0 0 0))
(foreach point #LstOfPoints
(setq tmp (mapcar '+ tmp point))
)
(mapcar '(lambda (x) (/ x (length #lst-of-points))) tmp)
)
Zum Schluss programmieren wir auch diese Funktion etwas eleganter und zwar in Verbindung mit apply.
; Agrumente
; #lst-of-points = Liste mit Punktkoordinaten
; sexy coded by Rolf Wischnewski (www.cadmaro.de)
(defun :M-RegularPolyCenter (#LstOfPoints)
(mapcar '(lambda (x) (/ x (length #LstOfPoints)))
(apply 'mapcar (cons '+ #LstOfPoints))
)
)
Und mit dieser Funktion können wir selbstverständlich auch den Mittelpunkt eines Dreiecks berechnen.
Beispiele
(:M-RegularPolyCenter (list (getpoint) (getpoint) (getpoint)))
=> (9.60022 2.23283 0.0)
(:M-RegularPolyCenter
'(
(10.9244 2.32568)
(10.9117 2.40369)
(10.8429 2.44246)
(10.7696 2.4128)
(10.7471 2.33703)
(10.7924 2.27222)
(10.8712 2.26716)
)
=> (10.837 2.35158)
Zum Schluß noch eine Ergänzung...
Man sollte unbedingt beachten, wie die Punkte übergeben werden, also entweder vom WCS oder vom UCS. Gegebenenfalls muß dann mittels trans der Mittelpunkt in das jeweilige Benutzerkoordinatensystem konvertiert werden.
Mit freundlicher Genehmigung von Rolf Wischnewski. Originalbeitrag im Februar 2006, CADmaro.de
